Alejandro de la Concha Duarte
Doctoral Researcher in Statistical Machine Learning

Contact: alejandro.d.delaconcha(at)gmail.com
I am Alejandro de la Concha, a PhD researcher in statistical machine learning at the École Normale Supérieure Paris-Saclay under the supervision of Prof. Nicolas Vayatis and Argyris Kalogeratos.
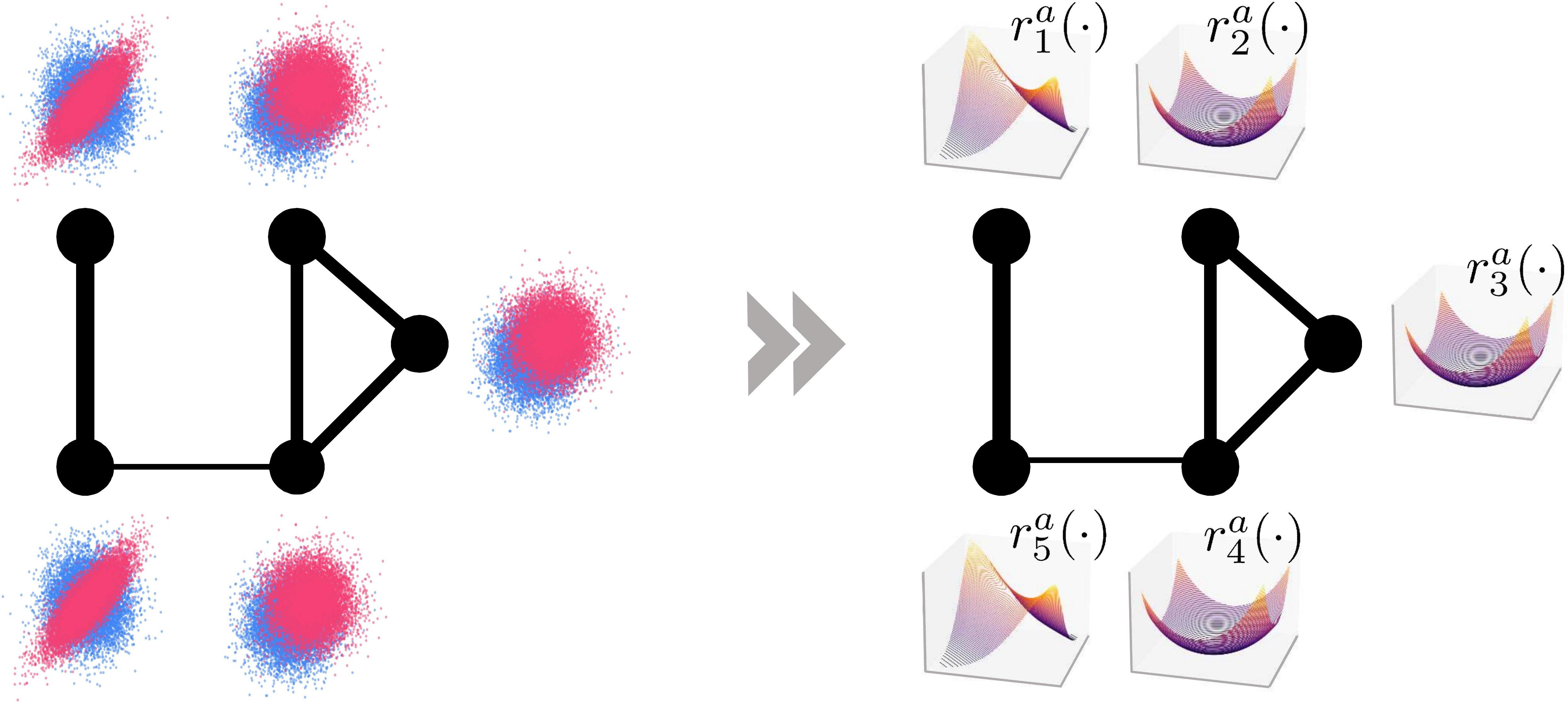
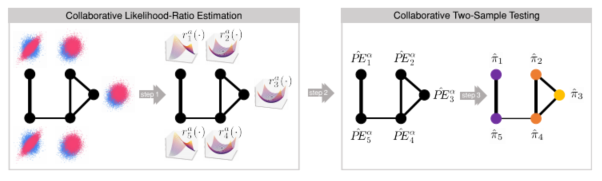
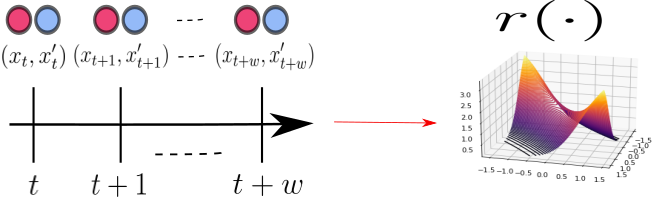
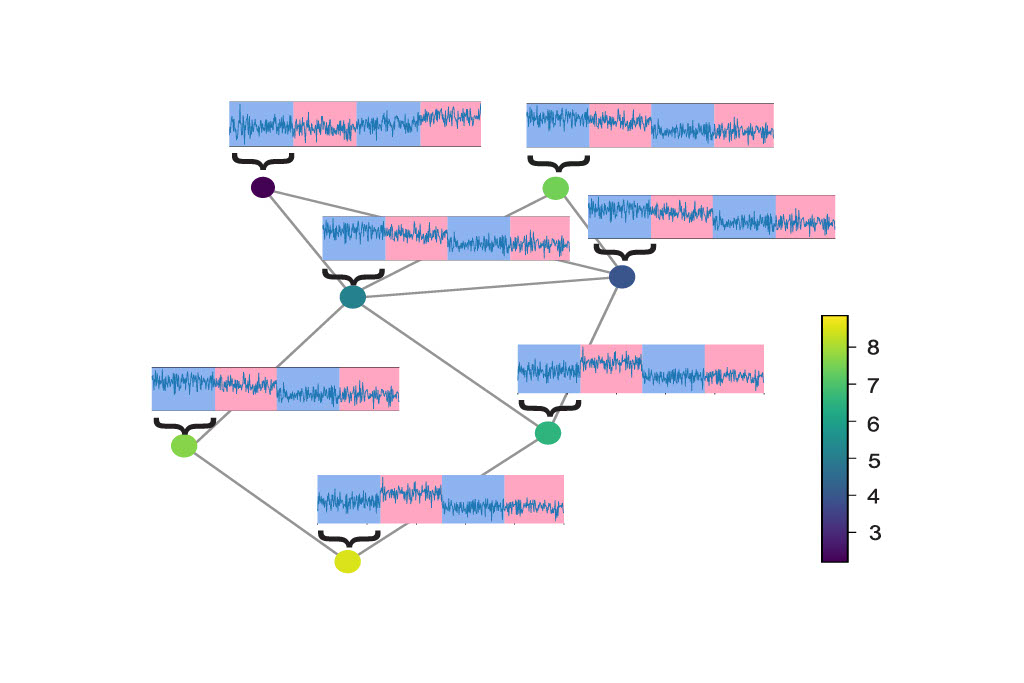
My thesis focuses on developing graph-based machine learning techniques for analyzing data generated in complex systems such as transport systems, financial networks, and sensor networks, to name a few. My work includes contributions to the subfields of: 1) Kernel methods and hypothesis testing. 2) Density/likelihood-ratio estimation. 3) Graph-signal processing.
Professionally, I have held positions in public and private institutions, where I have mainly focused on applying machine learning to risk management. I held a research data scientist position at Financial Network Analytics (FNA) and a financial risk analyst position at the Central Bank of Mexico (BANXICO) within the Directorate of Risk Management.